রহস্যময় সংখ্যা পাই (π )
(The Mystery of π )
—————- ড. রমিত আজাদ (Dr. Ramit Azad)
কয়েকদিন আগে পালিত হয়ে গেলো ‘পাই দিবস’। পাই-এর বহুল প্রচলিত মান যেহেতু ৩.১৪ তাই প্রতি বছর বছরের তৃতীয় মাস মার্চের ১৪ তম দিনটিকে পাই দিবস ধরা হয়। আমার জীবনে (সেই স্কুল জীবনে) প্রথম যখন পাই শব্দটি শুনলাম তখান আমাকে বলা হয়েছিলো যে পাই (π) একটি ধ্রুবক যার মান ৩.১৪। কি এই ধ্রুবক? কেন এর মান ৩.১৪? এই সব প্রশ্নের কোন ব্যাখ্যাই করা হয়নি। (এটা আমাদের বাংলাদেশের স্কুল শিক্ষার দুর্বলতা)। তার কিছুদিন পরে বই-পত্রেই দেখলাম π = ২২/৭। এটা ছিলো বিভ্রান্তিকর। কারণ ৩.১৪১৬ আর ২২/৭ এক নয়। তাছাড়া π একটি অমূলদ (অযৌক্তিক, Irrational) সংখ্যা আর ২২/৭ একটি মূলদ (যৌক্তিক, rational) সংখ্যা।
পিথাগোরাসের ছাত্র হিপাসাস আবিষ্কার করেছিলেন সেই জাতীয় সংখ্যা যাকে দুইটি পূর্ণ সংখ্যার অনুপাত হিসাবে প্রকাশ করা যায়না। পিথাগোরাস সেই সংখ্যাকে পছন্দ করেননি, তাঁর ধারনা ছিলো এ’জাতীয় সংখ্যা প্রকৃতিতে থাকতে পারেনা তাই তিনি সেই সংখ্যাকে বলেছিলেন irrational number-অযৌক্তিক সংখ্যা। অথচ আজ আমরা দেখি, irrational π-ই প্রকৃতিতে গুরুত্বপুর্ণ স্থান দখল করে আছে।
আসলে অপার রহস্যময় এই প্রকৃতি জগতের একটি রহস্যময় সংখ্যা এই পাই। সেই প্রাচীনকালেই এর রহস্য অনুধাবন করতে পেরেছিলেন আমাদের পূর্বপুরুষগণ, আর তার সাথে সাথেই চলেছে এর রহস্য উদঘাটনের প্রানান্ত প্রচেষ্টা।
রহস্যময় সংখ্যা π কখনো বৃত্তীয় ধ্রুবক, কখনো আর্কিমিডিসের ধ্রুবক আবার কখনও রুডলফের সংখ্যা যার পরিচয়। সেই রহস্যময় অমুলদ সংখ্যাটির মান জিজ্ঞেস করা হলে সবাই এক নিঃশ্বাসে বলে দিতে পারবো ৩.১৪১৬। π নিয়ে কমবেশি আমরা সবাই চিন্তা-ভাবনা করে থাকি। বলা হয়ে থাকে, পাইয়ের মাধ্যমে স্রস্টা আমাদের কিছু বোঝাতে চেয়েছেন। কিন্তু কি বোঝাতে চেয়েছেন তা বুঝতে হলে জানতে হবে π সম্পর্কে। যদিও তা নিয়ে জল্পনা কল্পনার শেষ নেই, তাই গবেষণারও কমতি নেই।
আমাদের দক্ষিণ এশিয়াতেই প্রথম পাইয়ের মোটামুটি সঠিক মান নির্ণয় হয়েছে বলে ধারনা করা হয়। ধারনা করা হয়ে থাকে যে দক্ষিণ এশিয় গণিতবিদ/দার্শনিকরাই প্রথম লক্ষ্য করেন যে কোন বৃত্তের পরিধি ও ব্যাসের অনুপাত একটি ধ্রুব সংখ্যা। তবে তারা সেই ধ্রুবের নাম কি দিয়েছিলেন সেটা জানা যায়নি। উপমহাদেশের প্রাচীনতম সভ্যতা সিন্ধু সভ্যতার কোন স্ক্রীপট-ই ডি-কোড করা সম্ভব হয়নি তাই সেই সময় পাই-এর জ্ঞান ছিলো কি না তা সঠিক করে বলা সম্ভব নয়। তবে ঋগবেদে পাই সম্পর্কে বলা আছে বলে মনে করা হয়। Vedangas ও Sulabasutras-তে পাই-এর উল্লেখ রয়েছে। Baudhayayana Sulabasutra-তে বলা হয়েছে বৃত্তাকৃতি কূপের পরিধি তার ব্যাসের তিন গুন। মহাভারতের Bhishmaparva, XII: 44-তে পাই-এর মান ৩ দেখানো হয়েছে। বেদের একটি কবিতায় আছে। ( there is a poem that is a hymn to Krishna which means)
: “O savior of those who have fallen, O lord Shiva, I beg you to protect me … ”
“Gopi bhagya madhuvrata
srngiso Dadhi sethiga khala
Jivita khatava
Gala hala rasetara ”
তবে এই কবিতার পিছনে গুপ্ত গণিত রয়েছে ।এখানে প্রতিটি সংস্কৃত ধ্বনি-ই একটি সংখ্যাকে প্রতিনিধিত্ব করে। সেই হিসাব করলে পাওয়া যায় 0.3141592653589 (But behind what appears to be simple, is hidden a real a secret of mathematics. In this poem, every sound in Sanskrit is a number and each sound has a numerical value from 0 to 9. In the 80’s, some scientists took these different sound values and applied them to this poem. A very significant number appeared: 0.3141592653589) … এটা হলো পাই-কে ১০ দিয়ে ভাগ করলে যা পাওয়া যায়।. পরবর্তিতে অনেক সুলভাসূত্র-তে উল্লেখ করা হয়েছে যে পাই-এর মান 18 * (3 – 2 √2) = 3.088। মানব সুলভাসুত্র-তে পাই-এর মান 28/5= 3.125 দেখানো হয়েছে। ১৫০ খ্রীষ্টপূর্বাব্দে প্রাচীন জৈন দর্শনে Π = √10 দেখানো হয়েছে। এছাড়া বরাহমিহির, ব্রহ্মগুপ্ত ও বাঙালী গণিতবিদ শ্রীধারা সহ অনেক জগতবিখ্যাত গণিতবিদই Π-কে ব্যবহার করেছেন। ৪৭৬ খ্রীষ্টাব্দে প্রতিভাধর গণিতবিদ ও জ্যোতির্বিদ আর্যভট্ট Π = 62832/20000 = 3.1416 দেখিয়েছিলেন। এটাই পরবর্তিতে চীনা গণিতে যুক্ত করা হয়েছিলো। ১৪০০ সালের দিকে মাধব (১৩৪০ থেকে ১৪৫০ খ্রীষ্টাব্দ পর্যন্ত) পাই নির্ণয়ের জন্য নিচের ধারা আবিস্কার করেন এবং এর সাহায্যে ১১ ঘর পর্যন্ত সঠিক মান নির্ণয়ে সফল হন।
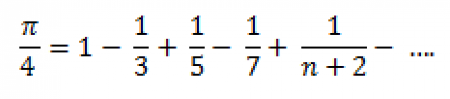
এই সিরিজটি ইউরোপে লেইবনিজ কর্তৃক পুণঃআবিষ্কৃত হয়েছিলো।
গিজার পিরামিডের উচ্চতা ও পেরিমিটার-এর এর মধ্যকার অনুপাত হলো ২π-এর সমান। সেখান থেকে অনেকে ধারনা করেন যে মিশরীয়-রাও π-এর মান জানতো। খ্রীষ্টপূর্ব ১৬৫০-এর মিশরের রিনড প্যপিরাসে বৃত্তের ক্ষেত্রফলের যে সূত্র পাওয়া গিয়েছে তা অনুযায়ী π এর মান (16/9)2 ≈ 3.1605। খ্রীষ্টপূর্ব ১৯০০-১৬০০ সালে তৈরী ব্যবিলনের একটি মাটির ট্যাবলেটে পাওয়া গিয়েছে যে π এর মান 25/8 = 3.1250। ইউক্লিড তার সমতলীয় জ্যামিতিতে, বৃত্তের পরিধি ও ব্যাসের অনুপাতকে π হিসেবে সংজ্ঞায়িত করেন, তবে তা কে আবিস্কার করে তা জানা যায়নি। খ্রীষ্টপূব ১৫০ সালে গনিতবিদ টলেমিও Π এর মান নিনয় করেছিলেন।
”…এবং তিনি এক গলিত ধাতব সমুদ্র (জলাধার) তৈরি করেন, যার এক প্রান্ত থেকে আরেক প্রান্ত ছিল ১০ কিউবিট দূরে। ইহা ছিল চতুর্দিকে গোলাকার যার উচ্চতা ছিল পাঁচ কিউবিট এবং পরিধি ৩০ কিউবিট লম্বা একটি সরলরেখার সমান।” – এটা হযরত সোলায়মান (আ: ) সম্পর্কে বাইবেলের একটি উদ্ধৃতি। বাইবেল অনুসারে কিং সোলায়মান (আঃ ) তার প্রাসাদের চত্বরে ধাতুর ব্যাবহারে একটি বিশাল আকৃতির বেসিন বা জলাধার তৈরি করিয়েছিলেন । বাইবেলের এই উদ্ধৃতি থেকে স্পষ্টত পাই এর মান ৩ পাওয়া যায়। হিব্রু স্ক্রীপ্ট অনুযায়ী সময়কালটি খ্রীষ্টপূর্ব অষ্টম থেকে তৃতীয় হতে পারে।
১৪২৪ সালে ইরানের মুসলিম জ্যোতির্বিদ জামশিদ আল কাশি ১৬ ঘর পর্যন্ত π-এর মান বের করলে মাধবের রেকর্ড ভেঙ্গে যায়। জার্মান গণিতজ্ঞ লুডলফ ভন চিউলেন আর্কিমিডিসের পর প্রথম ইউরোপীয় হিসাবে পাই গণনায় শরীক হোন। তিনি জ্যামিতিক পদ্ধতিতে দশমিকের পর ৩২ ঘর পর্যন্ত সঠিকভাবে পাই গণনা করেন। এই গণনা করে তিনি এত বেশি আনন্দিত ও গর্বিত হোন যে, মৃত্যুর পর তার সমাধিতে সেটি উৎকীর্ণ করা হয়। আইজাক নিউটন ১৫ ঘর পর্যন্ত পাইয়ের মান বের করেছেন। জন মাচিন হলেন প্রথম ব্যক্তি যিনি কী না ১০০ ঘর পর্যন্ত পাই-এর মান বের করেন।
১৭০৬ খ্রীষ্টাব্দে গণিতবিদ William Jones গ্রীক বর্ণ π-কে এই ধ্রুবকের প্রতীক হিসাবে ব্যব হার করেন এই কারণে যে periphery (περιφέρεια) (পরিধি)-র প্রথম বর্ণটির গ্রীক সিম্বোল/বর্ণ হবে π।
পাই এর রহস্যময়তা দিন দিন কেবল বৃদ্ধিই পেয়েছে। শুধু যে বৃত্তের পরিধি ও ব্যাসের অনুপাত এটা তা নয়। যেমন দুটো র্যান্ডম পূর্ণ সংখ্যার নিলে তাদের কোন সাধারণ গুণনীয়ক নাই তার সম্ভাবনা – 6/π2 (among a collection of random whole numbers, the probability that any two numbers have no common factor — that they are “relatively prime” — is equal to 6/π2)। আশ্চর্য্য!
পদার্থবিজ্ঞানে বর্নিত তরঙ্গেও পাই-এর দেখা মেলে। হাইজেনবার্গের অনিশ্চয়তার নীতিতেও পাই আছে।
একটি নদীর বক্রতার অনুপাত-এও পাই আসে। অর্থাৎ একটি নদীর প্রকৃত দৈর্ঘ্য ও লম্ব দৈর্ঘ্য এই দুয়ের অনুপাতও পাই। (pi emerges in the shapes of rivers. A river’s windiness is determined by its “meandering ratio,” or the ratio of the river’s actual length to the distance from its source to its mouth as the crow flies. Rivers that flow straight from source to mouth have small meandering ratios, while ones that lollygag along the way have high ones. Turns out, the average meandering ratio of rivers approaches — you guessed it — pi.)
জ্যামিতিতে বৃত্ত ছাড়াও গোলকের আয়তন ও তার উপরিতলের ক্ষেত্রফলের হিসাবেও পাই আসে।
বাস্তব ও কাল্পনিক সংখ্যার সংমিশ্রণ জটিল সংখ্যার বিশ্লেষণ-এও প্রায়শই পাই-কে দেখা যায়।
একটি সরল দোলকের পর্যায়কাল ও দৈর্ঘ্যের হিসাবেও পাই-এর দেখা মেলে। Electric constant থেকে শুরু করে magnetic constant পর্যন্ত বহু প্রাকৃতিক ধ্রুবকেই পাই এর সরব উপস্থিতি।
এবার আরো একটি বিষয় আলোচনা করব একটা অদ্ভূত পদ্ধতি নিয়ে যেটা বুফেন নেডেল পদ্ধতি নামে পরিচিত। ফরাসি গনিতবিদ Comet De Buffon এই পদ্ধতিতে Π এর মান বের করেন। তিনি প্রমান করেন-
π=2L/Pd
এ জন্য তিনি একটা কাগজ আর সূচ ব্যা্বহার করেন। কাগজটাতে নিচের চিত্রের মত কিছু সমান্তরাল দাগ কাটা থাকে এবং প্রত্যেক দাগ থেকে তার পাশের দাগের দুরত্ব সমান যেটা কে উপরের সমিকরনে d ধরা হয়েছে।এখানে L হচ্ছে সূচের দৈঘ্য যার মান অবশ্যই d থেকে ছোটো হতে হবে।
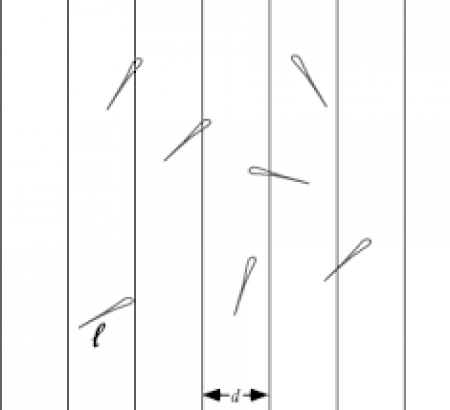
এখন, আমরা যদি সুচটাকে কাগজের উপরে বিনা বাধায় পরতে দেই, তাহলে সেটা কাগজের কোনো দাগ কে ছেদ করতে পারে নাও পারে, ধরা যাক, সুচটিকে ৫০ বার কাগজের উপরে ফেললে এটি ২৫ বার কোনো না কোনো দাগ কে ছেদ করে, তাহলে, এই সূচটির দাগ ছেদ করার সম্ভ্যব্যতা হবে ২৫/৫০=১/২ যেটাকে এই সমিকরনে P হিসেবে ধরা হয়েছে।
P= মোট ছেদের সংখ্যা/মোট নিক্ষেপের সংখ্যা
এখন আপনার পালা, আপনি যতবার ইচ্ছে তত বার সূচ নিক্ষেপ করে P এর মান বের করুন, এই মান গুলো উপরের সমিকরনে বসিয়ে পাই এর মান বের করুন। তবে একটা ব্যাপার, আপনি যত বেশি বার সুচ নিক্ষেপ করবেন, পাই এর মান তত ভাল আসবে। এখানে ইন্টারেস্টিং হলো পাই হচ্ছে একটা ধ্রব সংখ্যা যেটা পুরোপুরি নিশ্চিত আর সম্ভ্যব্যতা হচ্ছে পুরোপুরি অনিশ্চিত একটা ব্যাপার। আর এখানে অনিশ্চয়তার সাথে নিশ্চয়তার একটা গভীর সম্পর্ক দেখা যাচ্ছে। ইতিপূর্বে আমি কোয়ান্টাম মেকানিক্স নিয়ে বোর-আইনস্টাইন বিতর্ক শীর্ষক একটি আর্টিকেল লিখেছিলাম সেখানেও অনিশ্চয়তার সাথে নিশ্চয়তার একটি সম্পর্ক দেখানো হয়েছিলো।
যেহেতু প্রকৃতি জগতে পাই-এর এতো এতো সরব পদাচারনা তাই অনেকে এই সংখ্যাটিকে অতীব যৌক্তিক ও স্বর্গীয় মনে করে থাকেন।
—————————————-
কৃতজ্ঞতা স্বীকার: ইন্টেরনেটে প্রাপ্ত বিভিন্ন আর্টিকেল-এর সাহায্য নিয়েছি। সব লেখককে ধন্যবাদ।
পাই কে খুব ভালো পাই। লেখাটা খুব ভালো লেগেছে রমিত ভাই।
অনেক ধন্যবাদ নূপুর।
একবার মনে করেছিলাম, বুফন নীডল পদ্ধতি কীভাবে কাজ করে সেটা নিয়ে লিখব। গণিতের অনেকগুলো কনসেপ্ট আসবে লেখাটায়- ত্রিকোণমিতি, ক্যালকুলাস, সম্ভাব্যতা ইত্যাদি। পরে আর লেখা হয়ে ওঠেনি। আপনার লেখা দেখে মনে পড়ল। লেখাটা থেকে অনেক কথা জানলাম।
ধন্যবাদ গুলশান।